Introduction — quick roadmap and friendly start
Graphs and trees feel tricky at first. This article will make them simple. We will explain the difference between bfs and dfs in plain words. You will get clear examples. You will see short sample code and simple diagrams in words. The tone is friendly and calm. Sentences stay short so kids can follow. Each section focuses on one idea. You will learn when to use each search. You will learn time and space details too. By the end, you will feel ready to pick the right method. You can use these searches in games, maps, and puzzles. Ready? Let’s jump in and learn step by step.
What are BFS and DFS? — the basics in simple terms
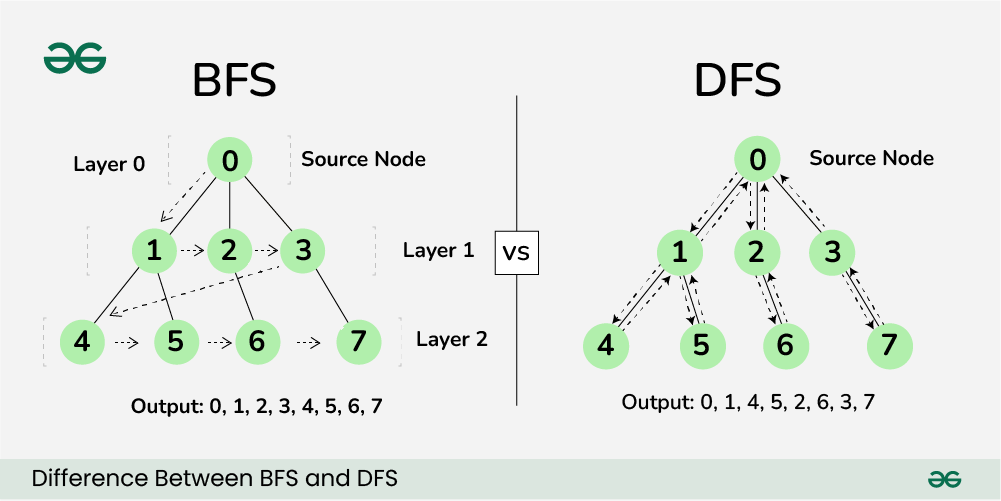
BFS stands for breadth-first search. DFS stands for depth-first search. Both are ways to visit every node in a graph or tree. BFS visits by layers. It checks all neighbors at one distance first. DFS goes deep along a branch before backtracking. BFS uses a queue to keep order. DFS uses a stack or recursion to dive deep. Both mark nodes as visited to avoid loops. They solve many problems in coding and logic. If you want the difference between bfs and dfs at a glance, BFS finds closer nodes first while DFS explores far paths fast. That short idea helps pick which to use.
How BFS works — step-by-step and easy mental picture
Think of BFS like waves at the beach. You stand at a start node. Then you visit every neighbor. Next you visit neighbors of those neighbors. You keep moving outward one layer at a time. BFS uses a queue. Add the start to the queue first. Remove front items and add their unvisited neighbors. Mark nodes visited to avoid repeats. BFS finds the shortest number of edges to every reachable node in an unweighted graph. A common use is level-order traversal of trees. If you wonder about the difference between bfs and dfs in order, BFS is level-focused. It is steady and broad. That helps when the shortest path matters.
How DFS works — step-by-step and clear image
DFS is like exploring a tunnel system. Start at a node. Pick one neighbor and go in. Keep going until you cannot go further. Then backtrack to the last choice point. DFS uses recursion or an explicit stack. Mark nodes visited to prevent cycles. This search traces a path deeply before trying other branches. DFS suits tasks that need full path exploration. It is handy for puzzles and for checking connectivity. When you ask about the difference between bfs and dfs in behavior, DFS prefers depth and paths. It can use less memory on sparse trees. But it may go very far before finding a near solution.
Traversal order and behavior differences — clear comparisons
The main visible gap is in order and how nodes are reached. BFS visits nodes by distance from the start. It lists nodes layer by layer. DFS visits nodes by following one path to its end. It then backtracks and tries other paths. Because of this, BFS finds the shortest path in terms of edges for unweighted graphs. DFS may find any path, not necessarily the shortest. The difference between bfs and dfs also shows in their typical data structure use. BFS uses a queue to remember the frontier. DFS uses a stack or function call stack to remember where to return. These patterns shape which algorithm fits which problem.
Time and space complexity comparison — practical numbers
Both BFS and DFS run in O(V + E) time on a graph. V is number of vertices. E is number of edges. That means both visit each node and edge at most once. The big difference lies in space. BFS can need O(V) extra space for the queue. In the worst case, one whole layer could be many nodes. DFS space is O(V) too in the worst case for recursion or stack. But often DFS uses less space for narrow graphs. When reading the difference between bfs and dfs, remember time is similar. Memory behavior and where they search are the key contrasts.
Implementation styles: iterative and recursive — simple code ideas
You can write BFS with a queue in iterative style. You push the start. While the queue is not empty, pop front and push neighbors. For DFS you can use recursion. Call a function that marks the node and then calls itself on each neighbor. Or write DFS iteratively with an explicit stack. Either way, the difference between bfs and dfs appears in code. BFS keeps nodes by level in the queue. DFS uses last-in, first-out order in a stack. Marking visited nodes early avoids infinite loops in cyclic graphs. Small, clean code helps avoid bugs.
Use cases for BFS — where it shines and why
BFS is ideal when you need the shortest path in an unweighted graph. Think of finding the fewest stops on a transit map. BFS finds the shallowest solution first. It is also great for level-order tree traversal. Use BFS to find nodes within a given distance. It helps in peer-to-peer networks and social graphs for friend suggestions at a distance. When you compare the difference between bfs and dfs, remember BFS is your go-to for shortest path and layer-based checks. It is predictable and fair. That predictability is often essential in real systems.
Use cases for DFS — when depth and structure matter
DFS is great for exploring possibilities, like solving mazes and puzzles. It finds a path quickly if one exists down a branch. DFS is used for topological sort in directed acyclic graphs. It helps detect cycles and find strongly connected components. DFS is often easier to implement with recursion. When thinking about the difference between bfs and dfs, know that DFS is better for full exploration and path-finding where depth matters. It can also be adapted for algorithms like backtracking and constraint search.
Choosing between BFS and DFS — rules of thumb
Pick BFS when the shortest path matters. Pick DFS when memory is tight or depth matters. If the graph is wide and shallow, BFS might use much memory. If the graph is deep and narrow, DFS will use less space. For unweighted shortest path problems, BFS is the natural choice. For puzzles with unique deep solutions, DFS often finds an answer quickly. The difference between bfs and dfs is not only theory. It is a practical guide you can use when designing programs. Try small examples in a debugger to see how each search behaves.
Graph representations and performance — adjacency list vs matrix
How you store a graph changes performance. An adjacency list stores only neighbors. It is memory efficient for sparse graphs. An adjacency matrix uses O(V²) space. It can be faster to check if an edge exists. Both BFS and DFS work with either representation. But the difference between bfs and dfs in runtime may be clearer with a list. With a list, iterating neighbors costs the degree of a node. With a matrix, iterating neighbors costs O(V) per node. For big graphs, adjacency lists plus either search is usually the best practical choice.
Advanced variants — bidirectional BFS and iterative deepening DFS
There are useful variants of both algorithms. Bidirectional BFS runs BFS from start and goal at once. It meets in the middle and can cut work dramatically. Iterative deepening DFS (IDDFS) repeats DFS with larger depth limits. It gets memory benefits of DFS with the shortest-path qualities of BFS for small depth. Other tweaks include heuristic pruning and limited-depth searches. When you study the difference between bfs and dfs, remember these variants blend strengths. They are common in game search and pathfinding systems where resources matter.
Common bugs and debugging tips — catch them early
A frequent bug is forgetting to mark visited nodes. This causes infinite loops in cyclic graphs. Another mistake is using recursion without considering depth. Very deep graphs can cause stack overflow. For BFS, forgetting to mark nodes when enqueued can add duplicates. Also watch how you manage neighbors and data structures. Use small test graphs to step through your code. Print the queue or stack during runs. That helps reveal the difference between bfs and dfs in action. Clear variable names and simple helper functions reduce errors.
FAQ 1 — What is the fastest way to find the shortest path?
For an unweighted graph, BFS is the simplest correct choice. It explores level by level. So the first time you reach the goal, you have the shortest path in edges. Algorithms like Dijkstra or A* handle weighted graphs. But if weights are equal, BFS wins for simplicity. When you ask about the difference between bfs and dfs for shortest path, BFS is what you want. DFS might find a path quickly, but not the shortest one. Also remember to reconstruct the path by storing parent nodes during BFS traversal.
FAQ 2 — Can DFS find shortest paths sometimes?
Yes, DFS can find a shortest path by chance. But it has no guarantee to do so. DFS follows a path deeply and stops when done. That path might be long. If you need the shortest path in an unweighted graph, DFS is not reliable. Comparing the difference between bfs and dfs, DFS is about depth, not closeness. There are special cases where DFS finds the shortest path, such as when the first path it explores happens to be the shortest. But rely on BFS when you need a guaranteed shortest route.
FAQ 3 — Which uses more memory usually, BFS or DFS?
Memory use depends on the graph shape. BFS can hold an entire level in the queue. If a graph has a very wide layer, BFS memory spikes. DFS stores nodes along a path in the stack or recursion. That is O(depth). In balanced trees, BFS may use more memory. In deep chains, DFS can use more. So the difference between bfs and dfs in memory is situational. Always reason about your graph shape before picking an algorithm.
FAQ 4 — How do I pick between recursive and iterative DFS?
Recursive DFS is concise and easy to read. Iterative DFS uses an explicit stack and avoids recursion limit issues. If your graph depth might exceed system recursion limits, prefer iterative DFS. Both approaches produce the same visiting order if you handle neighbors the same. When thinking of the difference between bfs and dfs, recursion is more tied to DFS style. But remember that recursion can hide state, so iterative code may be simpler to debug in some cases.
FAQ 5 — Are there cases where BFS fails but DFS works?
Not in terms of completeness on finite graphs. Both BFS and DFS will eventually visit all reachable nodes if implemented correctly. But performance matters. If you need a short path quickly, BFS will succeed faster. If memory limits keep BFS from running, DFS may finish where BFS cannot. So the difference between bfs and dfs shows in which one completes usefully. Also certain constrained problems need DFS variants, like depth-limited search, where BFS would be impractical.
FAQ 6 — Can BFS and DFS be combined in one algorithm?
Yes. Some algorithms mix ideas from both. Iterative deepening DFS acts like repeated DFS with increasing depth. Bidirectional search runs BFS from both ends. Heuristic searches like A* add best-first ideas. These hybrids aim to balance memory, speed, and path quality. The difference between bfs and dfs becomes a design choice. You can blend breadth and depth to suit a problem and available resources.
Conclusion — short recap and a call to action
Now you know the difference between bfs and dfs in order, memory, and use. BFS is layer-focused and finds shortest paths in unweighted graphs. DFS is path-focused and explores deep branches fast. Both run in linear time relative to nodes and edges. Your choice should match the problem shape and constraints. Try both on small graphs to feel the difference. Need help with code or a specific graph? Share your graph or a small sample. I can show step-by-step runs and working code for your case. Which example should we tackle next?